QA-LoRA: Quantization-Aware Fine-tuning for Large Language Models
Jointly fine-tune and quantize
State-of-the-art large language models (LLMs) are pre-trained with billions of parameters. While pre-trained LLMs can perform many tasks, they can become much better once fine-tuned.
Thanks to LoRA, fine-tuning cost can be dramatically reduced. LoRA adds low-rank tensors, i.e., a small number of parameters (millions), on top of the frozen original parameters. Only the parameters in the added tensors are trained during fine-tuning.
LoRA still requires the model to be loaded in memory. A billion parameters require 2 GB of memory. For instance, Llama 2 13B has 13 billion parameters so it requires 26 GB of memory. Note: This is assuming parameters with a 16-bit precision (fp16 or bfloat16). It requires twice as much memory if the model has 32-bit precision parameters (fp32).
Consumer GPUs have less than 24 GB of VRAM which is not enough to fine-tune most LLMs.
To reduce the memory cost and speed-up fine-tuning, a new approach proposes quantization-aware LoRA (QA-LoRA) fine-tuning.
In this article, I explain QA-LoRA and review its performance compared with previous work (especially QLoRA).
There is a lot to cover, so I wrote two articles. The next issue of The Kaitchup will be a tutorial in which we will see how to use QA-LoRA for fine-tuning Llama 2 and how it compares with QLoRA in terms of performance and computational cost (The current implementation of QA-LoRA is too unstable for a proper comparison with QLoRA. I’ll do this comparison later).
What’s Wrong with QLoRA?
Fine-tuning LoRA on top of a quantized LLM is something that we do very often here with QLoRA. I used it many times to fine-tune LLMs, for instance, Llama 2 and GPT-NeoX, on my desktop computer or using the free instance of Google Colab.
Before delving into QA-LoRA, it is interesting to understand what are the current limits of QLoRA.
The NormalFloat4 (NF4) Quantization
LLM quantization algorithms usually quantize parameters to a 4-bit precision using the INT4 data type. Computation with this data type is more and more optimized with recent GPUs.
QLoRA doesn’t use INT4 by default but another data type called NormalFloat4 (NF4). You can see it as a compressed float number. According to the authors of QLoRA, NF4 is superior to INT4. LLMs quantized with NF4 achieve a lower perplexity.
However, NF4 computation is not optimal for fast inference. This is one of the reasons why models quantized with GPTQ are faster than models quantized with bitsandbytes NF4. In previous articles, I confirmed that GPTQ models are indeed faster.
NF4 is also one of the weaknesses pointed out by the authors of QA-LoRA.
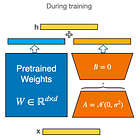
NF4 Base Model, But FP16 LoRA
While the base model is quantized with NF4, the trained LoRA’s parameters remain at a higher precision which is usually FP16, as illustrated in the figure below.
This is key in the QLoRA performance as naively training quantized parameters would lead to poor performance.
Consequently, for inference, we have two different ways to use the LoRA adapters trained with QLoRA:
Loading them on top of the base LLMs as we do during QLoRA fine-tuning
Merging them with the base LLMs
Loading them is optimal to preserve the performance. We keep LoRA’s parameters at 16-bit precision but, since they are only few millions, they don’t consume much VRAM relative to the quantized base LLMs.
The main issue is that we have then to deal with mixed-precision operations at inference time. In practice, quantized parameters of the base LLM are dequantized/quantize on the fly during inference to be used along with the FP16 parameters of LoRA. This further slows down inference.
The other alternative is to merge the LoRA’s parameters with the base model. I explored several merging recipes in a previous article.
We saw that ideally we have to dequantize the base model to the same precision used by LoRA’s parameters, and then merge LoRA’s parameters with the dequantized base model. I showed that it works and that the merged model performs as well as loading the LoRA adapter on top of the quantized base model.
But then, as a result, the merged model is not quantized anymore (FP16). It’s a big dequantized model. We could quantize the entire merged model but quantization always loses information. We would obtain a model performing below the performance we originally obtained at the end of the QLoRA fine-tuning.
Indeed, this is what I observed if you look at the last experiment in this notebook:
To sum up what I did:
Quantize the base LLM with NF4 (same quantization configuration used with QLoRA)
Dequantize the base LLM to the same precision used by LoRA
Merge LoRA with the dequantized LLM (at this point, the performance is optimal)
Quantize the merged LLM with NF4
The resulting model poorly performs (see the table below).
We can’t merge the QLoRA adapters, while preserving the quantization, without a significant performance drop.
Moreover, QLoRA dequantizes the parameters of the base model during the forward pass. It preserves fine-tuning stability and performance. But then, since the parameters are dequantized, QLoRA’s adapters can’t be “quantization-aware”.
Quantization-Aware Fine-tuning with QA-LoRA
QA-LoRA is presented in this arXiv paper:
QA-LoRA: Quantization-Aware Low-Rank Adaptation of Large Language Models (Xu et al., 2023)
This isn’t an easy paper to read. QA-LoRA is well-motivated and most of the results/experiments are convincing. But understanding why it works requires to be familiar with the mechanics behind quantization.
I won’t go deep into the mathematical theory and demonstrations here. I think the easiest way to understand QA-LoRA is to see it as a process jointly quantizing and fine-tuning LoRA’s parameters. The adapter’s parameters and quantization parameters are both learned, and applied, during the fine-tuning process.
To highlight the difference with QLoRA, we can refer to this paragraph from the paper:
We introduce group-wise operations, increasing the number of parameters of quantization from Dout to L×Dout, meanwhile decreasing that of adaptation from Din×Dint+Dint×Dout to L × Dint + Dint × Dout. As we shall see in experiments, a moderate L can achieve satisfying accuracy of language understanding meanwhile preserving computational efficiency.
In addition, QA-LoRA uses the standard INT4 data type while QLoRA uses NF4.
QA-LoRA Performance and Computational Cost
Let’s have a look at the performance reported by the authors of QA-LoRA. They report on many experiments but I think the following table is the one that gives the best overview of QA-LoRA performance, compared to QLoRA, and for various quantization precisions:
In this table, we have the performance of the original LLaMA 7B (16-bit) compared to:
Standard QLoRA with NF4 quantized base LLM and FP16 LoRA (denoted QLoRA”)
LLaMA 7B quantized with GPTQ to INT4 (denoted “LLaMA-7B w/ GPTQ”)
Merged QLoRA adapter quantized with GTPQ (denoted “QLoRA w/ GPTQ”)
QA-LoRA
The standard QLoRA performs the best. This is expected since it uses a very good data type for quantization (NF4) while LoRA’s parameters remain FP16.
We can see that when we want to merge QLoRA adapters and then quantize the merged models (QLoRA w/ GPTQ), the performance significantly drops. Again, as we discussed in the previous section of this article, this is expected.
QA-LoRA on the other hand performs almost as well as the standard QLoRA while the LLM is entirely quantized with INT4. In other words, QA-LoRA works.
What’s more is that QA-LoRA is more flexible than QLoRA by allowing fine-tuning with LLMs quantized to the lower precisions. QA-LoRA with 3-bit precision is superior to QLoRA merged and quantized to 4-bit (60.1% accurracy for QA-LoRA 3-bit against 59.8% for QLoRA w/ GPTQ 4-bit).
Overall, QA-LoRA results look very impressive.
As for the computation cost, this is were I found the paper less convincing. They propose the following experiment:
According to this table, QA-LoRA fine-tunes faster than QLoRA. But, in my opinion, these results are somewhat misleading and I’m not sure what the authors actually want to show here. The “time” is (approximately) twice higher than QLoRA but on the other hand QA-LoRA fine-tunes (approximately) twice less parameters (for LLaMA 7B/13B). Naively, I would say that this is normal. If we fine-tune less parameters, we should expect the fine-tuning to be faster.
In the next issue of The Kaitchup, I will present my own benchmarking of QA-LoRA. I will also show you how to use QA-LoRA with Llama 2. This is not complicated and the authors provides an implementation that is built on top of auto-gptq, a library that I have already used in previous articles.











Why is QLoRA better than the base model? Because it has more training?