Hi Everyone,
In this edition of The Weekly Kaitchup:
“LoRA without Regret” and Rank=1
Granite 4.0 in The Kaitchup Index
Tiny Recursive Models for Very Specific Problems
“LoRA without Regret” and Rank=1
One of the most surprising takeaways from the Thinking Machines article we covered in last week’s Weekly Kaitchup is that GRPO-style reinforcement learning with a LoRA rank of 1 can match the performance of full GRPO (i.e., updating all weights). As expected, several people tried to validate this. Hugging Face shared a replication setup, and it seems to partially hold for their SmolLM 3 model:
LoRA Without Regret (by Hugging Face)
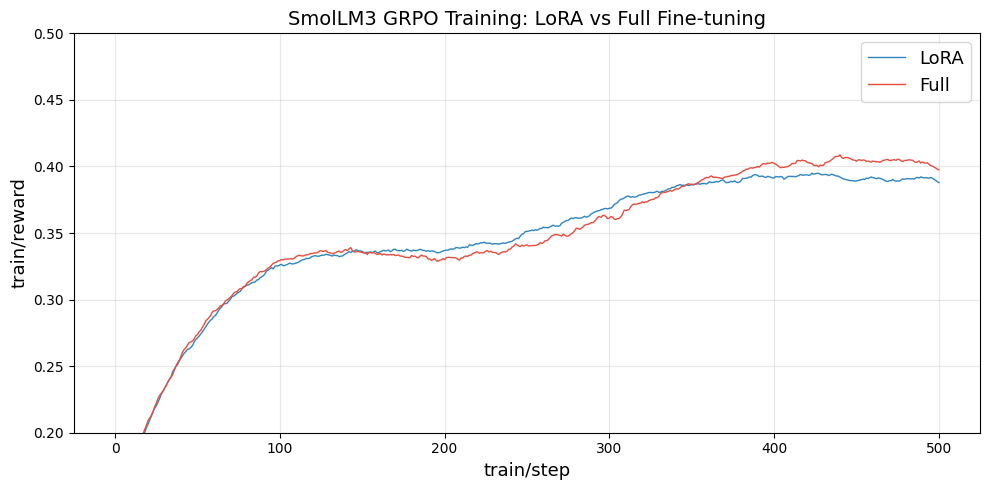
They got some good-looking learning curves confirming that LoRA with rank 1 is good:
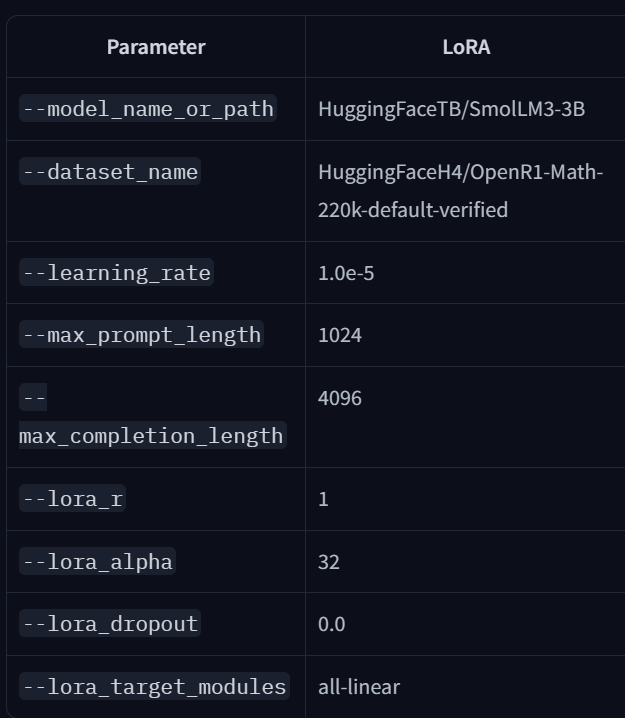
They used the following configurations applied to Qwen3-0.6B:
peft_config = LoraConfig(
r=1,
lora_alpha=32,
target_modules=”all-linear”
)
training_args = GRPOConfig(
learning_rate=5e-5,
per_device_train_batch_size=1,
gradient_accumulation_steps=4,
num_train_epochs=1,
num_generations=8,
generation_batch_size=8,
report_to=[”trackio”],
)Early on, the curves overlap, LoRA (rank = 1) even leads briefly, but full fine-tuning pulls ahead and stays there. So rank-1 LoRA doesn’t behave identically to full training in practice. That doesn’t refute Thinking Machines’ claim that rank = 1 can be sufficient. Still, it suggests the training dynamics (optimizer, schedule, regularization, etc.) likely create a gap that keeps full training ahead, and it may not be trivial to close.
Let’s look at their hyperparameters:
These settings largely mirror Thinking Machines’. I’d be curious to see a domain beyond math: every successful rank-1 report I saw this week used math datasets. It’d be valuable to test other tasks, especially with datasets that were not generated by LLMs, or with noisier, harder-to-verify rewards.
Last week, I also ran rank-1 experiments using Unsloth’s new notebook to train GTP-OSS:
GRPO Training for GTP-OSS with Unsloth
Note: The notebook currently points to misnamed modules. As written, it only applies LoRA to self-attention and skips the expert layers. With rank = 1, that leaves ~500k trainable parameters, versus ~11.5M if all experts were correctly targeted.
The training objective in this notebook by Unsloth is quite original:
Our goal is to make a faster matrix multiplication kernel by doing RL on GTP-OSS 20B with Unsloth.
They define several reward functions for the task, worth reading in the notebook and trying yourself.
In my runs, I compared rank = 1 vs. rank = 64: the higher rank performed notably better. Rank-1 does learn (which is remarkable), but it didn’t reach the same reward as rank-64. These are preliminary results. I’m preparing a full write-up and will re-verify everything. I’m also testing non-math tasks like translation.
Granite 4.0 in The Kaitchup Index
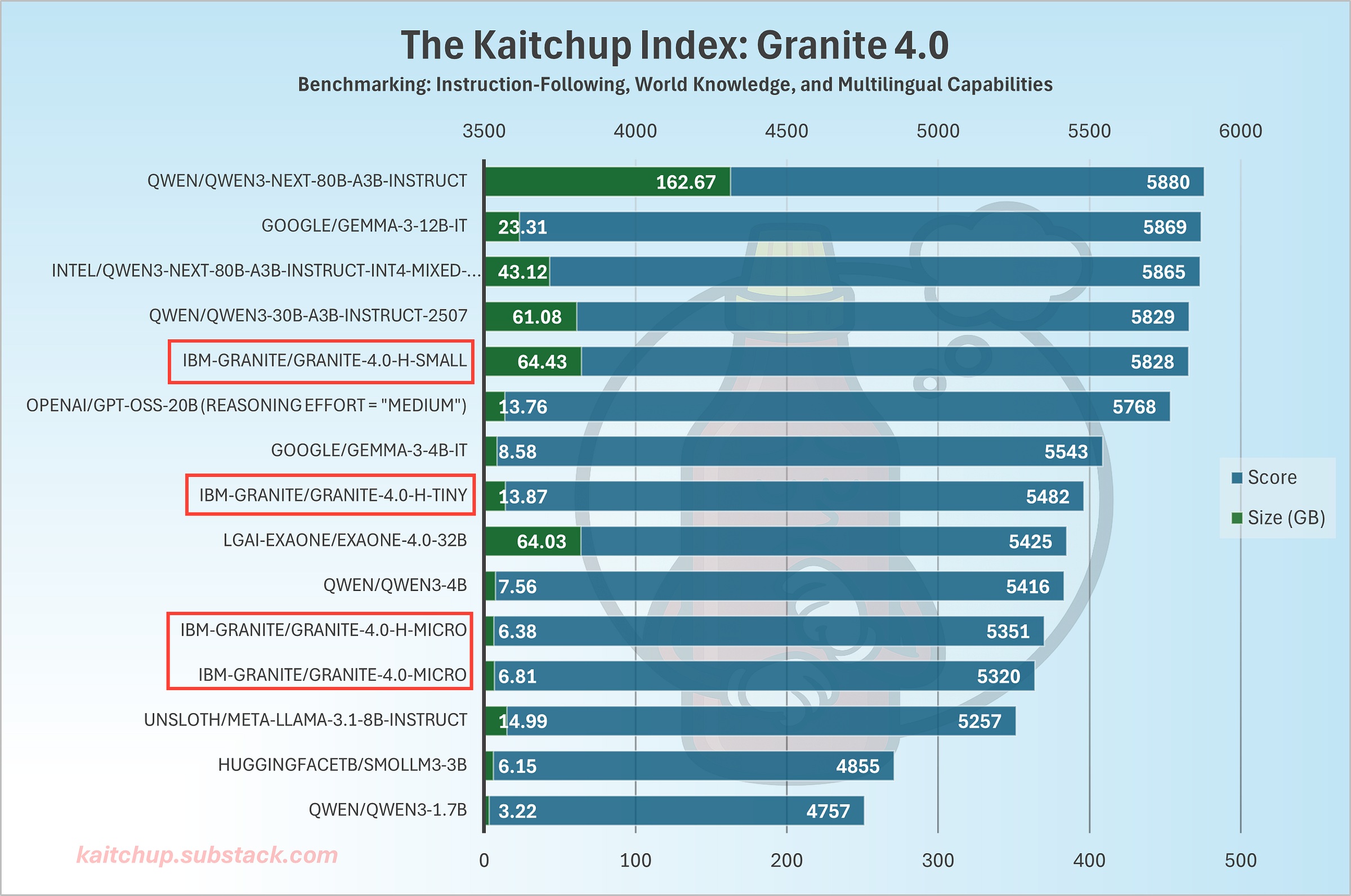
I added IBM’s Granite 4.0 models to the Kaitchup Index, which is my own private benchmark unseen by the models during training. Here is how they perform among comparable models (full results here):
The Small variant matches the recent Qwen3-30B-A3B despite being a hybrid model with Mamba-2 layers. H-Micro also performs well, between Qwen3-4B and Qwen3-1.7B, which is consistent with its 3B parameter size. As a hybrid, it’s also more inference-efficient than those Qwen3 models.
Surprisingly, the dense Micro underperforms the hybrid version, a pattern IBM also reports. IBM notes the dense release exists primarily for frameworks that don’t yet support Mamba-2, so it may not have been trained as long or as carefully as the hybrid models. I don’t think there is a good use case for it.
Tiny Recursive Models for Very Specific Problems
Interesting paper by Samsung trending this week:
Less is More: Recursive Reasoning with Tiny Networks
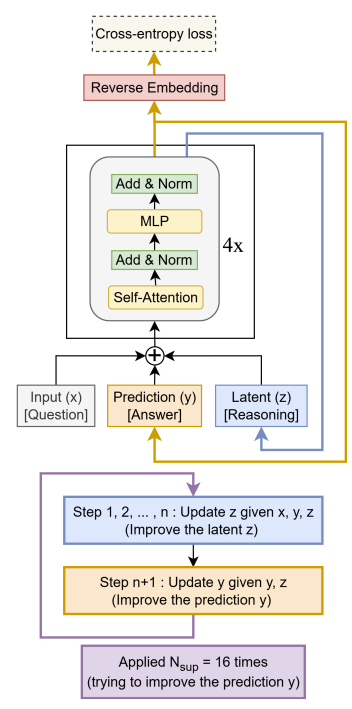
The work argues you can solve tough, structured puzzles with tiny, recursive networks instead of huge LLMs. It revisits HRM (two small transformers that recurse at different rates) and proposes Tiny Recursive Model (TRM): a single, 2-layer network that repeatedly refines a latent state and the current answer.
Despite just ~7M parameters and ~1K training examples per task, TRM reports strong gains: Sudoku-Extreme (up to 87.4% test accuracy), Maze-Hard (85.3%), ARC-AGI-1 (44.6%), and ARC-AGI-2 (7.8%), often surpassing HRM and several large proprietary LLMs under the authors’ setup.
What’s wrong (or unclear) with HRM
HRM’s appeal is “hierarchical recursion” plus “deep supervision,” but most of the benefit comes from the deep supervision. The two-rate recursion adds little. The paper also questions HRM’s reliance on a fixed-point justification for backpropagating through only the final steps, arguing that those fixed points are not actually reached in practice. And while HRM uses Adaptive Computational Time (ACT) to cut average steps per example, its implementation adds an extra forward pass each iteration, which the author frames as a practical training cost.
Definition: Adaptive Computational Time
ACT lets a model decide, per input (often per token), how many internal steps to run before stopping. A learned “halting” signal accumulates until a threshold is reached, while a small “ponder cost” penalizes extra steps, encouraging more compute on hard cases and less on easy ones. This yields variable-depth inference that can cut average latency without hurting accuracy.
How TRM simplifies and strengthens the recipe:
One tiny network, two roles: the same module improves a latent “reasoning” state and then refreshes the current answer.
Full backprop through a whole recursion: no fixed-point assumption, and just run several lightweight refinement cycles and backprop through the last one.
Replace HRM’s ACT with a single learned halt signal, avoiding the extra pass.
Regularization for tiny data: use EMA, prefer 2 layers with more recursion rather than deeper models, and on Sudoku’s short grids, an attention-free MLP head beats self-attention.
The evaluation is interesting but leaves room for caution. Results rely on heavy data augmentation and specific training schedules, and comparisons against LLMs feel “customized” (e.g., fixed attempts on ARC, particular decoding/compute choices). The reported gains on Sudoku and Maze look robust under their setup, while ARC-AGI remains hard even for TRM. It would help to see broader ablations on parsing choices, alternative halting schemes, and sensitivity to augmentation strength across seeds and hardware.
The paper concludes:
Currently, recursive reasoning models such as HRM and TRM are supervised learning methods rather than generative models. This means that given an input question, they can only provide a single deterministic answer. In many settings, multiple answers exist for a question. Thus, it would be interesting to extend TRM to generative tasks.
The Salt
The Salt is my other newsletter that takes a more scientific approach. In The Salt, I primarily feature short reviews of recent papers (for free), detailed analyses of noteworthy publications, and articles centered on LLM evaluation.
I reviewed in The Weekly Salt:
⭐Fine-Tuning on Noisy Instructions: Effects on Generalization and Performance
Large Reasoning Models Learn Better Alignment from Flawed Thinking
Group-Relative REINFORCE Is Secretly an Off-Policy Algorithm: Demystifying Some Myths About GRPO and Its Friends
That’s all for this week.
If you like reading The Kaitchup, consider sharing it with friends and coworkers (there is a 20% discount for group subscriptions):
Have a nice weekend!